
跳出来很关键
绝大多数事物都不简单。高维度不仅是历史发展的大趋势,而且自有其好处。
如前文所说,从低维看高维存在难度,那么从高维看低维,效果如何?
考虑以下情况(见图1-7 ):如果试图从一个正方形内的一点A到达正方形外的一点B ,同时又保持在这张纸所在的平面上,那么就必定要穿过封闭的围线C 。但如果我们利用三维空间,离开这张纸所在的平面,那就不必穿过围线C了。
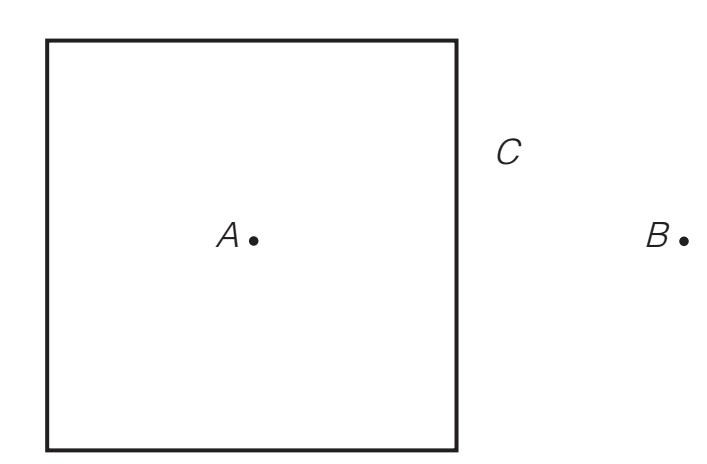
图1-7 正方形外的一点
这就是从二维平面“跳出来”,利用第三维来解决问题──“跳出来”很关键。
这个抽象的法则,有一个生动的现实版本。法国科学家法布尔( Fabre )在《昆虫记》里记载了他的一次试验(见图1-8 ):
有一天,我看到很大一群毛虫爬到花盆上,渐渐地来到它们最为得意的盆沿上。慢慢地,这一队毛虫陆陆续续到达了盆沿,在盆沿上前进着。我等待并期盼着队伍形成一个封闭的环,也就是说,等第一只毛虫绕过一周而回到它出发的地方。一刻钟之后,这个目的达到了。现在有整整一圈的松毛虫在绕着盆沿走了。……于是我就把还要继续上去的毛虫拨开,然后用刷子把丝线轻轻刷去,这相当于截断了它们的通道。这样下面的虫子再也上不去,上面的再也找不到回去的路。这一切准备就绪后,我们就可以看到一幕有趣的景象在眼前展开了:
一群毛虫在花盆沿上一圈一圈地转着,现在它们中间已经没有领袖了。因为这是一个封闭的圆周,不分起点和终点,谁都可以算领袖,谁又都不是领袖,可它们自己并不知道这一点。
丝织和轨道越来越粗了,因为每条松毛虫都不断地把自己的丝加上去。除了这条圆周路之外,再也没有别的什么岔路了,看样子它们会这样无止境地一圈一圈绕着走,直到累死为止?
……
松毛虫们继续着它们的行进,接连走了好几个钟头。到了黄昏时分,队伍就走走停停,它们走累了。当天气逐渐转冷时,它们也逐渐放慢了行进的速度。到了晚上十点钟左右,它们继续在走,但脚步明显慢了下来,好像只是懒洋洋地摇摆着身体。……第二天早晨,等我再去看它们的时候,它们还是像昨天那样排着队,但队伍是停着的。晚上太冷了,它们都蜷起身子取暖,停止了前进。等空气渐渐暖和起来后,它们恢复了知觉,又开始在那儿兜圈子了。
……
第六天……这时盆沿上的毛虫队已不再是一个完整的圆圈,而是在某处断开了。也正是因为有了一个唯一的领袖,才有了一条新的出路。……实验的第八天,由于新道路的开辟,它们已开始从盆沿上往下爬,到日落的时候,最后一只松毛虫也回到了盆脚下的巢里。
毛毛虫在盆沿上爬了8天,就是因为它们的“线性思维”,或者说是“一根筋的思维”。

图1-8 毛毛虫是怎样饿死的
在低维情况下的另一案例,是理论家们假想出来的二维动物──如果世界上存在二维动物,那么它们根本不能吃东西,否则就会被消化道劈成两半(无论它长得像鸟,还是像其他动物,下场都一样)。
幸亏动物是三维立体的,才避免了被活活饿死的尴尬──增加一个维度,就能解决低维的困境。
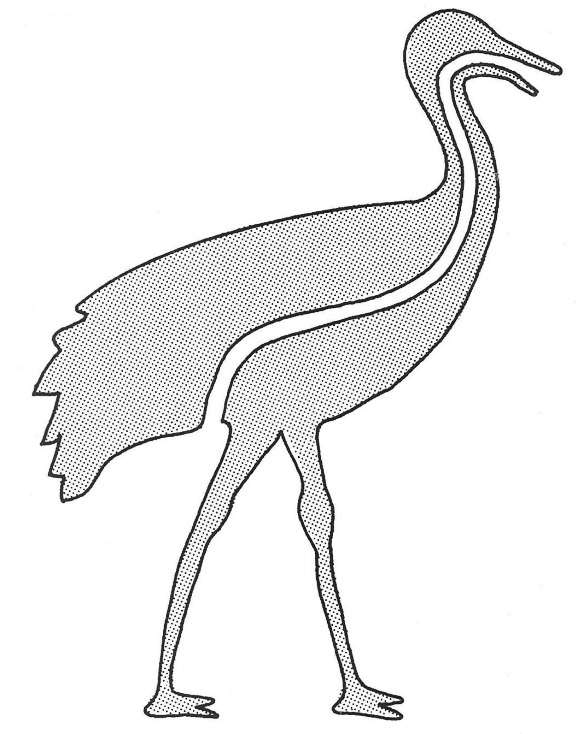
图1-9 不能吃东西的二维动物
资料来源:引自加来道雄(Michio Kaku)的著作《超越时空:通过平行宇宙、时间卷曲和第十维度的科学之旅》(Hyperspace: A Scientific Odyssey Through Parallel Universes, Time Warps, and the 10th Dimension )。
人类生活在三维空间中,但仍有自身的困境,能否通过增加维度来解决呢?比如,从一个立方体内的一点A到立方体外的一点B ,必须穿过立方体的表面(如果我们限于三维空间中)。但是,与平面情形相类似,如果我们利用一下第四维,那就不必穿过立方体表面了(见图1-10 )。

图1-10 立方体外的一点
也许有人会问:立方体中的A点怎么就到了外面的B点?不知道,反正在另一个时间点上,它出现在B点!听上去无厘头吗?回想一下前文四维的模拟动态图1-6 ,只要它能利用时间维度“动”起来,里面的就到了外面,外面的就到了里面!
这还算简单的,在科学史上对维度的研究比这复杂得多,而且不断增加维度似乎是一种常态。
布赖恩·格林( Brian Greene )在《宇宙的结构:空间、时间以及真实性的意义》( The Fabric of the Cosmos: Space, Time, and the Texture of Reality )一书中提到这样一段历史: 1919年,爱因斯坦收到了一篇论文,这篇论文出自当时还没有什么 名气的 德国数学家西奥多·卡鲁扎( Theodor Franz Eduaqrd Kaluza )之手。卡鲁扎恳请爱因斯坦和物理学家们接受宇宙有四个空间维度的可能性。他怎么会有这么古怪的想法?爱因斯坦为什么没直接把这篇论文扔进垃圾堆呢?原因在于卡鲁扎发现爱因斯坦的广义相对论方程在更高维度宇宙同样适用,而且在高维宇宙中扩展后又有了一些新的方程;更奇怪的是,这居然就是19世纪麦克斯韦发现的用以描述电磁场的方程!宏观世界和微观世界的原理就在增加一个维度后出现了统一的迹象!
过了几十年,卡鲁扎的这个古怪想法逐渐由其他研究者演化为弦论,似乎要求有九个空间维度。为什么是九个?由于弦论中的方程要求某些条件能被精确地满足,这在三维、四维、五维、六维、七维、八维甚至七千维中都无法实现,但在十维时空(九维空间加一维时间)中却能被完美地满足!
到了1995年,弦论学家爱德华·威滕( Edward Witten )发现还少了一个维度,因为人们在20世纪七八十年代使用的是近似方程,弦理论就出现了五种看似各不相同的版本。威滕发现如果再增加一个维度,就可以将它们统一为M理论,而先前的五个版本都是它的不同组成部分。
图1-11引自《宇宙的琴弦》( The Elegant Universe , 布赖恩·格林的另一本关于超弦理论的经典著作),它形象地体现了先前五种弦论(图1-11 a )
和后来的M理论(图1-11 b )之间的关系。这不是很像盲人摸象故事的“科学版”吗?
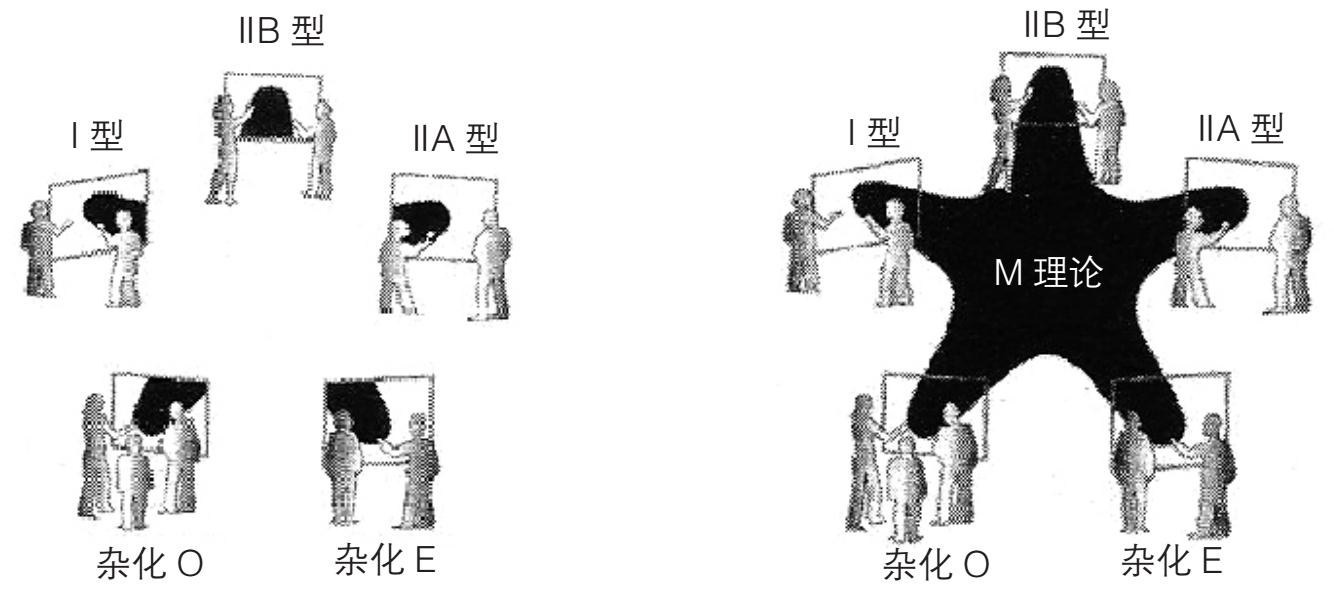
图1-11 M理论的拼装
尽管威滕获得的重大发现是与之前的理论研究路数一脉相承的(只是利用额外维度罢了),但是当他在1995年的年度国际弦论会议上抛出他的结果时,还是让包括格林在内的整个研究领域的学者感到强烈震动。
由此可见,维度真是个好东西!思维要突围,就要增加维度。“思维”二字本身就包含“维”,或许正意味着“维度”──复杂思维通常是高维度的思维,而且维度的增加常常会带来惊喜。
维度原理在生活中是非常实用的。在新闻学领域,有“ 5W1H ”的说法,即在报道一个新闻事件时常常会包含以下要素: Who (什么人)、 When (什么时候)、 Where (什么地点)、 What (什么事)、 Why (为什么)、 How (怎么样)。用“ 5W1H ”基本能描述世界上的任何一个事件。换言之,世界上的任何一个事件,都包含这些基本维度。我们不妨把它画成一张图(见图1-12 )。
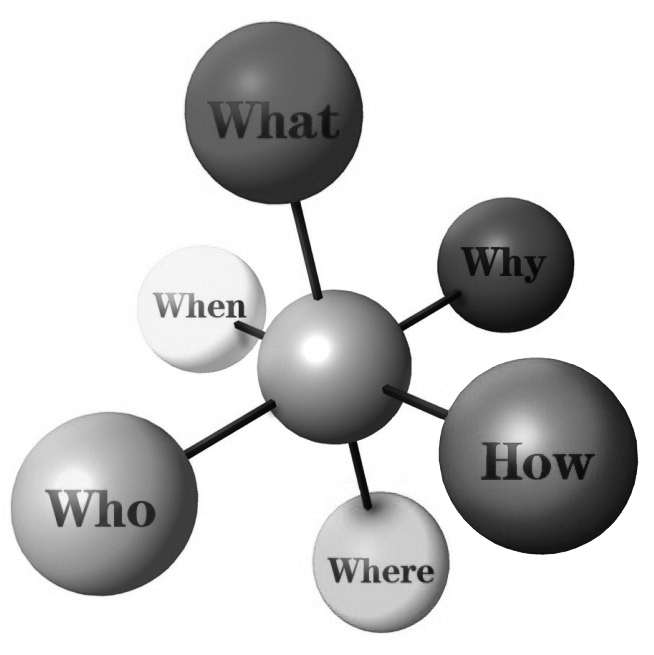
图1-12 六个维度
2013年,有一个高考状元从香港大学退学,就是因为对该校的教学环境不满意,希望能到北京大学学中文,于是退学后再一次参加高考,这是在“ Where ”上做文章。
如果上述这些都做不到,那么能否改变心态,把酷暑当作锻炼意志品质的一种手段?这就是改变看待它的方式“ How ”。比如, 2013年的一条社会新闻,南方某高校的学生为抵挡酷暑买了个大冬瓜当抱枕,这种苦中作乐的心态,想必多年之后必将成为他宝贵的人生经历。
所以,在“ 5W1H ”中任意改变一个或几个条件,困境就有望得到化解。高维度的好处是能帮我们从困境中突围,让我们确信:“困难年年有,办法总比困难多!”


